Actividad integradora
El chorro de agua
Para realizar esta actividad, es necesario leer y
comprender los temas: 1, 2, y 3. Así como realizar los ejercicios que se
presentan en el tema, ya que ahí encontrarás los referentes teóricos para poder
resolver esta actividad, en conjunto con el análisis de la situación y la
aplicación de lo aprendido. Esta información, te permitirá resolver, de manera
autónoma, los problemas planteados.
¿Qué producto entregarás?
Un documento donde presentes las respuestas a cada una de
las preguntas planteadas, incluyendo el procedimiento que seguiste para
resolver las situaciones.
¿Qué hacer?
1. Resuelve el siguiente problema.
Desarrolla el procedimiento e incorpora la solución.
A un tinaco de 1.27 m de alto se le hace un pequeño
agujero debido al tiempo y la corrosión,este agujero se encuentra justo en la
base del tinaco. Deduce la fórmula para calcular la velocidad con que saldrá el
chorro de agua por el agujero y calcula.
Desarrollo:
 |
DATOS:
V2 H2 P2
V21= Volumen
P=Presión
p= Densidad del agua
g =
gravedad = 9.81 m/s2 ( El valor promedio en la superficie de nuestro
planeta se convierte en una constante)
h= 1.27 m
La velocidad en el punto más alto es
insignificante comparada con la velocidad del chorro,es decir: pv
/
2 = 0, entonces la expresión queda:
Al realizar la multiplicación
P*V1= 0 * 0 = 0
Al
elevar la segunda velocidad nos da V2
=02 =0
V1
*1000 gr/cm3=0
La expresión queda: P1+pgh1=
P2 + pV 22 / 2 +pgh2
La presión en ambos puntos es aproximadamente
la misma, es decir: P1=P2 o P1-P2 =
0, entonces la expresión resultante es:
P1+pgh1=
P2 + pV 22 / 2 +pgh2
Si
pasamos P2 hacia el lado izquierdo pasa en negativo y da un igual a P1-P2 =
0 por lo cual
La expresión queda: pgh1=
pV 22 / 2 +pgh2
De la expresión anterior
considera que la altura en el punto más bajo es cero por lo que ρgh2 = 0,
entonces la expresión simplificada queda como:
pgh1= pV
22 / 2 +pgh2
h2=0
Multiplicamos altura 2 * densidad * altura
h2
* p * g = 0
La expresión queda: pgh1= pV 22 / 2
Despejando la velocidad de esta última expresión, la
velocidad la podemos calcular con la fórmula:
pgh1= pV
22 / 2
lo
primero que se hace al no haber sumas se divide en densidad
pgh1=
pV 22 / 2
p p
de esta manera nos quedaría gh1=V22 /2
Multiplicamos ambos lados * 2 2 * gh1=V22 /2 * 2
Y nos quedaría 2 * gh1=V22
Para eliminar de el volumen que lo eleve al cuadradro
sacaremos raíz cuadrada
de ambos lados √ 2 * gh1= √ V22
nos damos cuenta que la raíz cuadrada nos dice que v22 es inversa se elimina y
nos quedaría una expresión V2= √ 2gh1 por
lo tanto la respuesta es la b)
a) v2=(2gh1)2
b) v2=
c) v2=2gh1
Sustituye el valor de la altura del tinaco y calcula la
velocidad con la que el agua sale por el agujero:
En este caso solo seguiremos los pasos que nos indica la
formula adquirida en la pregunta anterior:
V2= ¿ ?
h = 1.27 m
g= 9.81 m/s2
v2=
= √2
* 9.81 m/s2 * 1.27m = √ 24.91 m2 /
s2 = 4.99 m/s
= √2
* 9.81 m/s2 * 1.27m = √ 24.91 m2 /
s2 = 4.99 m/s
la velocidad con la que sale
el agua es V2= 4.99 m/s
4. Anota cada pregunta con su respectiva
respuesta y el procedimiento que seguiste en cada caso, guarda el documento y
sube tu archivo a la plataforma con el siguiente nombre:
Apellidos_Nombre_M12S1_El chorro de agua
En la presente actividad has desarrollado tus habilidades
para:
Diferenciar funciones matemáticas de primer y segundo
grado utilizando los conceptos (densidad, presión, presión hidrostática, flujo
volumétrico) y principios (Arquímedes, Pascal, Bernoulli y Torricelli) de los
fluidos que se abordan en esta unidad, para apoyar su comprensión.
Comprender las expresiones matemáticas (ρ=m/V, P=F/A, PH=
ρgh, E= ρLVLg, Ec=mv2/2,
F1/A1=F2/A2, v2=2gh) que representan conceptos y
principios que describen el comportamiento de los fluidos, para aplicarlos en
problemas prácticos o experimentos relacionados con estos fenómenos físicos,
presentes en su ciudad, país o mundo.
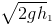
No hay comentarios:
Publicar un comentario